Currently, START-PROF can run seismic analysis according to following seismic design codes:
SNiP II-7-81* Building in seismic zone code
SP 14.13330.2018 Building in seismic zone code
NP-031-01 Nuclear plants seismic design code
GB50011-2001 Code for seismic design of buildings
User defined acceleration
Responses from the following forces are considered in piping seismic resistance analysis:
From inertial forces
From piping deformation during seismic waves in soil (for buried pipelines)
Then total responses from all components of seismic and static components are calculated.
Pipeline analysis for seismic effects from inertial forces use the following methods:
Equivalent static method (used in START-PROF)
Linear-spectral theory of seismic resistance
Dynamic analysis method
Equivalent static method - assumes response calculation based on equivalent static inertial loads for various directions of seismic effects. This method is superior to the linear-spectral theory in the analysis simplicity and the ability to consider a structural non-linear system (disabling of single-directional restraints), which cannot be considered in the linear-spectral theory. It is inferior in that higher structure vibration modes cannot be considered. Therefore, to account for the possible inaccuracy in seismic load analysis, safety margins are added and seismic acceleration is set as equal to maximum spectral acceleration.
Linear-spectral theory - gives more accurate results compared with the equivalent static method, gives smaller piping responses due to more accurate assessment of seismic acceleration depending on structure frequency values. This theory uses initial seismic effects as an acceleration spectrum based on which modal inertial seismic loads (corresponding to each frequency) are calculated. These loads are applied as static and modal responses are calculated. Then design response is calculated as a sum of all modal responses using special formulas.
Dynamic analysis method - gives more accurate results, considers physical, geometric and structural non-linearity; but is much more labor and knowledge intensive in practice. This method is used for especially critical pipelines. Soil seismic acceleration records (accelerograms) must be input. Analysis uses either a direct integrated movement formula, or structure movement is separated into individual frequencies and vibration modes. In other words, piping movements during the earthquake and following it are modeled. During modeling, maximum responses values at different points in time are fixed.
Currently, the equivalent static analysis method is implement in START-PROF, which allows analysis of seismic resistance with some margin. Inertial forces are calculated using
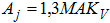
1.3 - static method correction factor taking into account inaccuracy compared with the linear-spectral theory (considering higher vibration modes);
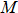- piping element mass
(node concentrated or uniform mass along the pipe length);
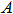- (Alpha1 for GB50011-2001) maximum
spectral acceleration value, calculated considering selected
standard requirements
(SNIP II-7-81*,
SP 14.13330.2018, NP-031-01, GB50011-2001);
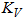- vertical
seismic acceleration factor set in START-PROF input
data. Usually taken in
0.65-0.75 range.
If piping is located on ramp, building etc., then seismic accelerations should be multiplied by factor kh. In horizontal direction:
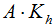
In vertical direction:
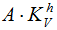
Factors should be determined according to codes.
Six additional seismic load cases are run to calculate responses from inertial forces:
L1: Operation static loads from all loads W+P+T
L2: Operation static loads from weight W+P
L3: "+X" from operation static loads and inertial forces directed positively along the X axis
L4: "-X" from operation static loads and inertial forces directed negatively along the X axis
L5: "+Y" from operation static loads and inertial forces directed positively along the Y axis
L6: "-Y" from operation static loads and inertial forces directed negatively along the Y axis
L7: "+Z" from operation static loads and inertial forces directed positively along the Z axis
L8: "-Z" from operation static loads and inertial forces directed negatively along the Z axis
Structural non-linearity (enabling/disabling supports with single-directional restraints and supports with gaps), pendulum effect (rod rotation) and friction are taken into account.
Results can be obtained in results tables:
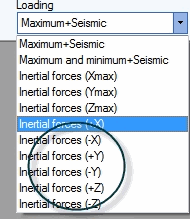
Maximum responses for each of seismic force direction are calculated using the internal forces difference between operation static loads (L1) analysis and operation static + inertial loads analysis (L2-L7):
L9, L10: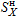 
maximum responses from "+X" and "-X" L3-L1,
L4-L1
L11, L12: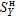 
maximum responses from "+Y"
and "-Y" L5-L1, L6-L1
L13, L14: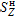 
maximum responses from "+Z" and "-Z" L7-L1,
L8-L1
Results can be obtained in results tables:
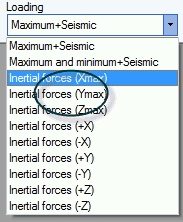
For SRSS(X,Y,Z) method the displacements, support loads, expansion joint deformations etc. 2 seismic cases are calculated as
L12. L1 + (max(L9,L10)^2 + Xmax_SAM^2 +max(L11,L12)^2 + Ymax_SAM^2 +max(L13,L14)^2 + Zmax_SAM^2)^0.5
L13. L1 - (max(L9,L10)^2 + Xmax_SAM^2 +max(L11,L12)^2 + Ymax_SAM^2 +max(L13,L14)^2 + Zmax_SAM^2)^0.5
Xmax_SAM, Ymax_SAM, Zmax_SAM - seismic anchor movements responses, see below.
Stresses are calculated as:
L12. L2 + (max(L9,L10)^2 + Xmax_SAM^2 +max(L11,L12)^2 + Ymax_SAM^2 +max(L13,L14)^2 + Zmax_SAM^2)^0.5
SUS - sustained load case
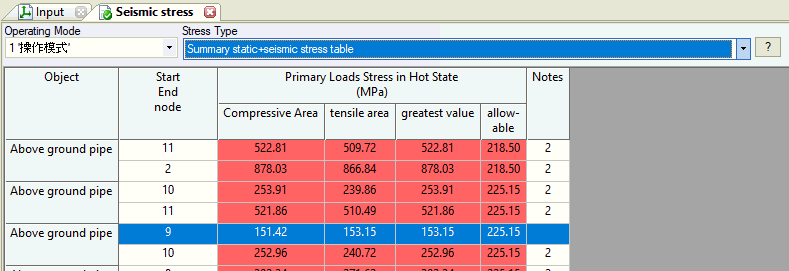
Note: the stresses are calculated separately for tensile and for compressive area. The absolute maximum stress result is used in further calculations.
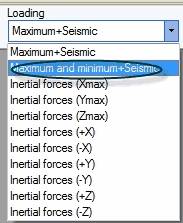
For MAX(X,Y,Z) metod the displacements, support loads, expansion joint deformations etc. 6 seismic cases are calculated as
L12. L1 + max (L9, L10, L11,L12, L13, L14, Xmax_SAM, Ymax_SAM, Zmax_SAM)
L13. L1 + min (L9, L10, L11,L12, L13, L14, Xmax_SAM, Ymax_SAM, Zmax_SAM)
Stresses are calculated as:
L12. L2 + max (L9, L10, L11,L12, L13, L14 Xmax_SAM, Ymax_SAM, Zmax_SAM)
Maximum absolute responses are calculated as:
L14. max (abs(L12), abs(L13))
When calculating seismic stresses - 2 zones are checked: Compressive area and Tensile area. It is important for several piping stress analysis codes, where axial force and bending moment are considered.
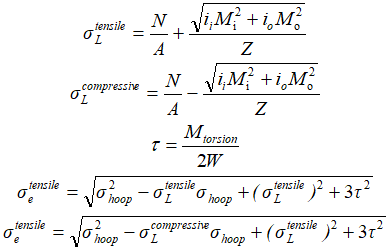
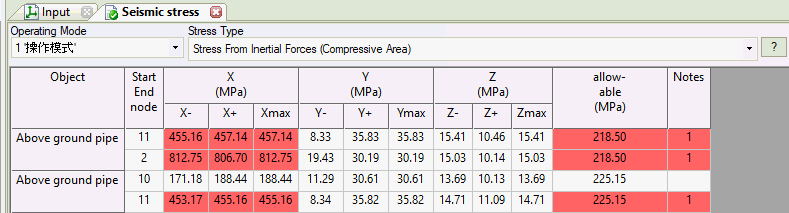
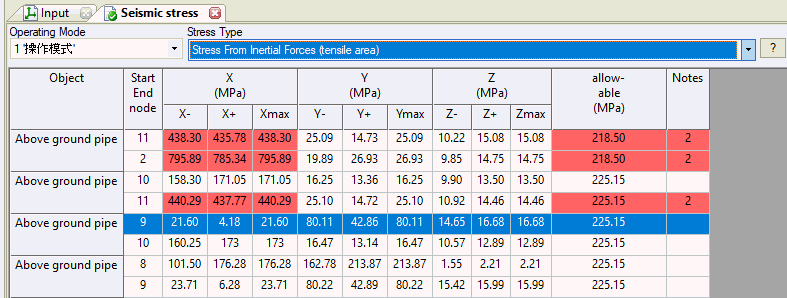
Tensile and compressive area stresses are calculated separately and greatest value is taken at the end of calculation process.
Piping can be connected to several points on a building, attached to one or more heavy structures (buildings, vessels and equipment, tanks, etc.), which may move during an earthquake independent of each other and the piping. In this case, in addition to inertial forces from piping vibration, additional static loads caused by mutual displacement of restrained points will be applied.
To determine static load components, seismic support displacement values and direction must be known. For this, supports can belong to one or more "phase groups". For example, all supports on the same floor of a build move synchronously, so they belong to phase group 1. Supports on another floor belong to phase group 2. Phase group number is unlimited. Each phase group moves independently of other groups.
Phase group displacement values can be obtained by seismic effects analysis of the corresponding structure; for example, using specialized structural analysis software.
Seismic anchor movements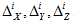 
is maximum possible
values in X,Y and Z direction that happen at different moments of time.
For each phase group, three maximum allowable displacement values (at different points in time) along the XYZ axes must be input. Six seismic load case analysis are done for each phase group:
L15: "+X" from operation static loads and displacement of all supports in this phase group by value X positively along the X axis
L16: "-X" from operation static loads and displacement of all supports in this phase group by value X negatively along the X axis
L17: "+Y" from operation static loads and displacement of all supports in this phase group by value Y positively along the Y axis
L18: "-Y" from operation static loads and displacement of all supports in this phase group by value Y negatively along the Y axis
L19: "+Z" from operation static loads and displacement of all supports in this phase group by value Z positively along the Z axis
L20: "-Z" from operation static loads and displacement of all supports in this phase group by value Z negatively along the Z axis
For second phase group:
L21: "+X" from operation static loads and displacement of all supports in this phase group by value X positively along the X axis
L22: "-X" from operation static loads and displacement of all supports in this phase group by value X negatively along the X axis
L23: "+Y" from operation static loads and displacement of all supports in this phase group by value Y positively along the Y axis
L24: "-Y" from operation static loads and displacement of all supports in this phase group by value Y negatively along the Y axis
L25: "+Z" from operation static loads and displacement of all supports in this phase group by value Z positively along the Z axis
L26: "-Z" from operation static loads and displacement of all supports in this phase group by value Z negatively along the Z axis
Structural non-linearity (enabling/disabling supports with single-directional restraints and supports with gaps) and pendulum effect (rod displacement from vertical position) and friction are taken into account.
Maximum responses for each movement direction are calculated using the internal forces difference between operation static loads (L1) analysis and operation static + inertial loads analysis (L2-L7):
1 phase group:
L27: S_i_x=max(|L15-L1|, |L16-L1|)
L28: S_i_y=max(|L17-L1|, |L18-L1|)
L29: S_i_z=max(|L19-L1|, |L20-L1|)
2 phase group:
L30: S_i_x=max(|L21-L1|, |L22-L1|)
L31: S_i_y=max(|L23-L1|, |L24-L1|)
L32: S_i_z=max(|L25-L1|, |L26-L1|)
Then, the final three responses are calculated as square roots of a sum of squares for all phase group restraints:
L33: Xmax_SAM=(L27^2+L30^2+...)^0.5
L34: Ymax_SAM=(L28^2+L31^2+...)^0.5
L35: Zmax_SAM=(L29^2+L32^2+...)^0.5