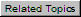

1 - backfill soil, 2 - expansion cushion, 3 - foundation soil
Fig. 1
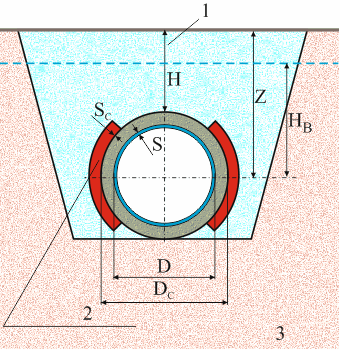
Axial stress σz in PUR insulation is calculated using equation:
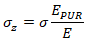
where
σ - axial stress in the steel pipe (from bending and axial force)
Е - elastic modulus of the steel pipe
ЕPUR - PUR elastic modulus.
Maximum shear stress along the pipeline axis τyz due to friction of the polyethylene shell against soil occurring on the surface of the PUR layer attached to the external steel pipeline surface equal to:
Where qfr - longitudinal uniform friction force, Dc - PE casing diameter.
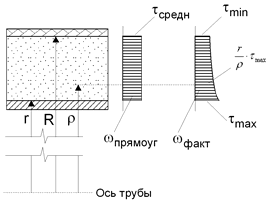
To determine the radial σy, circumferential σx, and shear stresses τxy of the PUR layer, a 1cm ring cut out of the pipe in a flat deformed state is analyzed using built-in finite element method engine into START-PROF (fig. 2). The stresses are calculated in 5 points around the pipe.
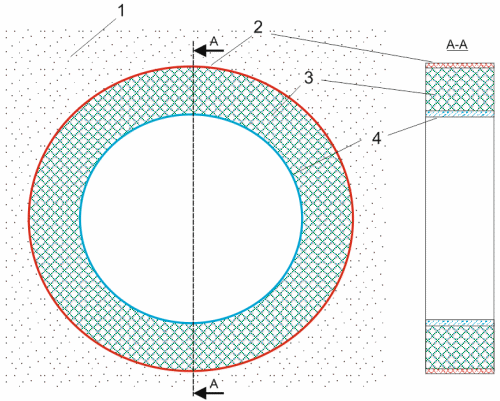
1 - foundation soil, 2 - polyethylene casing, 3 - foamed polyurethane, 4 - steel pipe
Fig. 2
Maximum shear stress τxy take place at the internal layer of PUR thickness
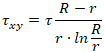
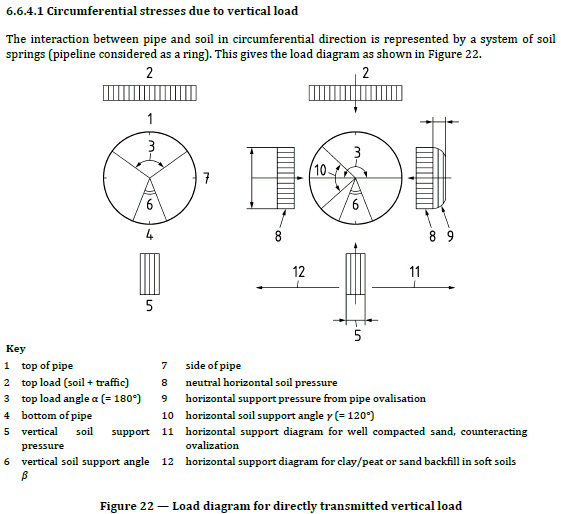
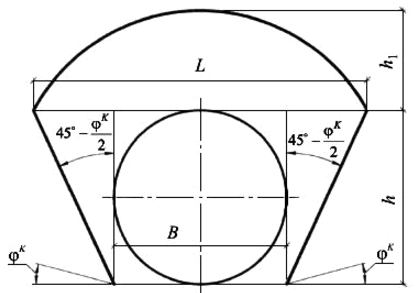
Soil pressure is divided into two parts: vertical and horizontal. Vertical load is equal to soil layer pressure for the corresponding depth and applied only to the top half of the ring, while base elastic properties determined by analysis act on the lower half. Horizontal load is distributed along the trapeze and is equal to vertical pressure multiplied by the lateral pressure factor (fig. 4).
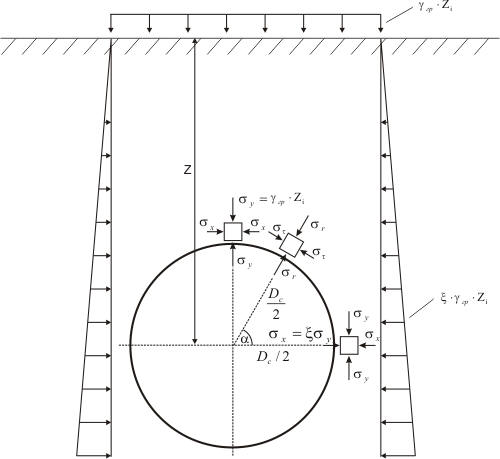

Fig. 4
If open trench type laying is used, then chosen, then soil natural arch of collapse is not considered. The soil pressure on the pipe is calculated using whole depth. The soil pressure increases linearly with increasing depth.
If trenchless laying method is used, and the pipe depth is very high, then a self-supporting arch collapse forms above the pipe (natural arch of collapse). This arch supports all the soil pressure above itself. Only soil inside the natural arch of collapse produce the pressure on the pipe.

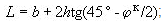
Soil is modeled as discrete springs around PE casing finite element model. The springs are working only for compression, any spring will be switched off in case of tension. The soil peeling usually take place at the top of the pipe cross-section due to cross-section ovalization, so several springs at the top of the pipe usually are not working.
Also internal pressure and product hydrostatic pressure is applied acting in radial direction on each point of pipe perimeter. The finite element analysis consider geometric nonlinearity, therefore the effect of additional ring stiffening caused by internal pressure is also considered.
Five stress tensor components are calculated σx, σy, σz, τyz, τxy, τxz=0 (fig. 5). Equivalent stress is determined based on the theory of greater sheer stress as a difference between the first and third principal stress:
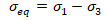
where σ1 and σ3 are roots of the equation
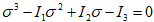
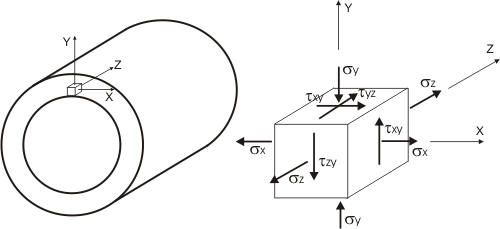
Fig. 5
Equivalent and shear stresses are calculated in 5 different points of PUR insulation A, B, C, D, E (fig. 6)
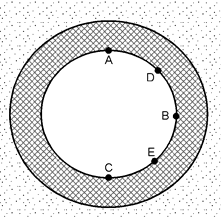
Fig. 6
According to 7.3.1, 7.3.2 EN 13941, 4.5.5.2 EN 253 and GOST 55596, allowable equivalent stress for PUR insulation layer, circumferential and longitudinal shear stresses are checked to guarantee PUR layer strength and adhesion to steel pipe. Allowable stress for PE casing is 12 MPa
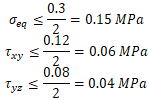
During analysis, a non-linear equation system is solved. Non-linearity is due to accounting for detachment of the elastic base modeling soil in the top part of the pipe and the presence of internal pressure (considering geometric stiffness due to pressure). In some cases, iteration may not produce results. There can be two causes:
Insufficient pipe wall thickness. In this case, wall thickness stability may be lost due to pressure of the surrounding soil. A warning regarding insufficient wall thickness for stability conditions will be given.
Insufficient base soil carrying capacity. If the base soil stiffness is insufficient for the given model, pipe balance in soil may be lost since the system becomes instantly-changing. This is due to the fact that elastic springs without non-linear properties model soil. In this case, turning on the function to increase base soil stiffness is recommended to ensure pipe stability.
See also Ring Bending Stress Calculation
1. Alexandrov A.V., Magalif V.Y., Matveev A.V., Stress analysis of foamed polyurethane insulation, «Pipelines and ecology», 2003, №3, ZAO «NPO Stroypolimer»
2. GOST 30732-2006, Steel pipes and fittings with foamed polyurethane insulation in polyethylene casing, Gosstroy of Russia, 2006
3. GOST 55596-2013 District Heating Network Stress Analysis