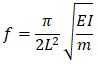
Read about START-PROF pipe stress analysis software
Modal analysis (natural frequency analysis) measures the response of a piping system to dynamic loads. Dynamic loadings have a tendency to increase the response of the structure beyond the response obtained if the same load was applied statically. The natural frequencies of a piping system should not be close to the equipment operating frequencies.
If piping natural frequency is close to the equipment operating frequency, the resonance effect occurs and vibration amplitudes become too great. The goal is to reduce or increase the piping natural frequencies by adding the supports, changing design, using rigid supports instead of flexible, etc.
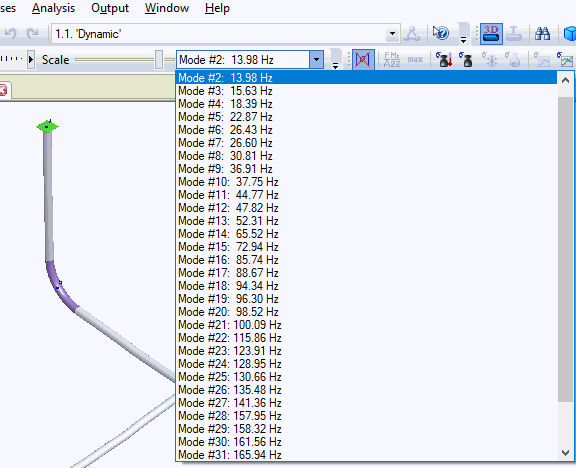
Usually making the natural frequencies higher is better solution than making them lower. START-PROF calculates the natural frequencies and periods and show the animated mode shapes.
To perform modal analysis, please toggle the check box "dynamic" in the operation mode editor for the appropriate operation mode.
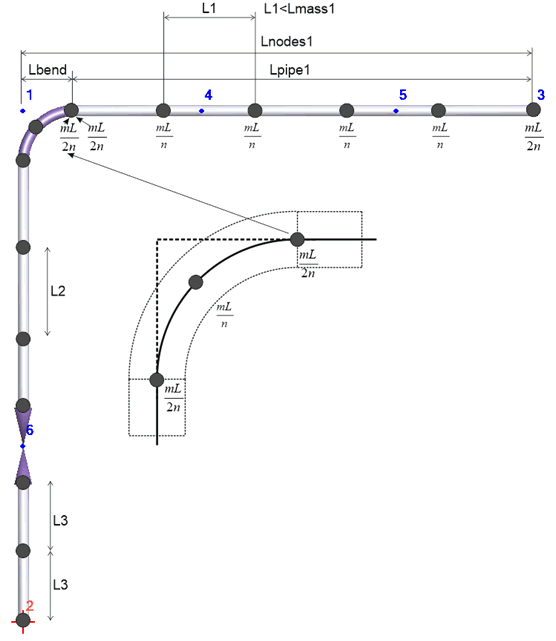
START-PROF uses lumped mass model. But the inertial forces are uniformly acting on every pipe span. To receive the accurate analysis results the masses must be properly discretized. START-PROF use the algorithm for automatic insertion of masses into the piping system, additional intermediate invisible nodes with masses are automatically added into the pipe elements. The maximum span between masses is calculated based on the first natural frequency (f) of an equivalent simply supported beam:
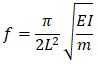
In case of 2 masses per span, the optimum pipe length (L) will be:
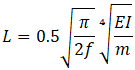
where:
f - cut-off frequency. Specified by user in project settings. Default value is 33 Hz.
m - mass per unit length of pipe. Include pipe mass, insulation, contents and additional weight
E - modulus of elasticity of pipe material
I - moment of inertia of pipe cross section
If the pipe or bend arc length is greater than the optimum element length (L), the additional lumped masses are inserted in order to make the actual distance between points less than or equal to the optimum L. Also masses are automatically added into bends (3 or more masses), tees (1 or more masses), reducers (2 masses). If valve or flange length is less than 0.5L then 1 mass added, if greater then 2 masses added.


Dynamic analysis in START-PROF is applicable only on linear systems, so any non-linearities must be linearized before running the dynamic analysis:
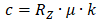
where
k - is a friction coefficient for dynamic analysis, 1/mm (or other length units). This factor can be adjusted to make the dynamic model behavior similar to the actual dynamic response of the real system.
The default value is 40 1/mm (1000 1/in). Enter k=0 to ignore friction in the analysis. Use great value like k=10000 to consider friction as rigid restraints.
Rz is a restraint load from operation mode static analysis, m is a friction factor
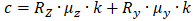
where Rz is a vertical load, mz is a friction factor for vertical load, Ry is a horizontal load, my is a friction factor for horizontal load
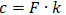
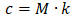
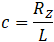
where Rz is vertical load on hanger and L is hanger length
The undamped frequencies and modes of free vibration of piping structure are obtained by the solution of generalized eigenvalue problem:
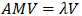
where:
A - flexibility matrix
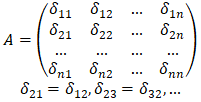
V - matrix of mode shapes
M - mass matrix
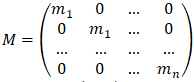
l - eigenvalue, that is equal to
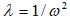
w - Angular Frequency, Rad/s
There are three mass degrees of freedom per node with mass element, rotational mass is ignored. After dynamic piping model is ready, START-PROF runs the Dynamic Eigensolver, which calculates natural frequencies and modes of vibration. The processor searches for the natural frequencies, starting with the lowest, and continues until the requested number of natural frequencies is reached the requested.
After analysis if finished, you can review natural frequencies and mode shapes in Natural Frequencies and Periods table.
Angular Frequency, Rad/s
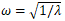
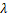 - Eigenvalue obtained from
Eigensolution
- Eigenvalue obtained from
Eigensolution
Technical Frequency, 1/s (Hz)
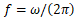
Period, s
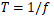
You can also display the mode shapes in and animated format in Output 3D View Window.