

Read about START-PROF Pipe Stress Analysis Software
The START-PROF has a very powerful and detailed, but easy to use and fully automatic soil model. Software user's manual work is reduced to minimum.
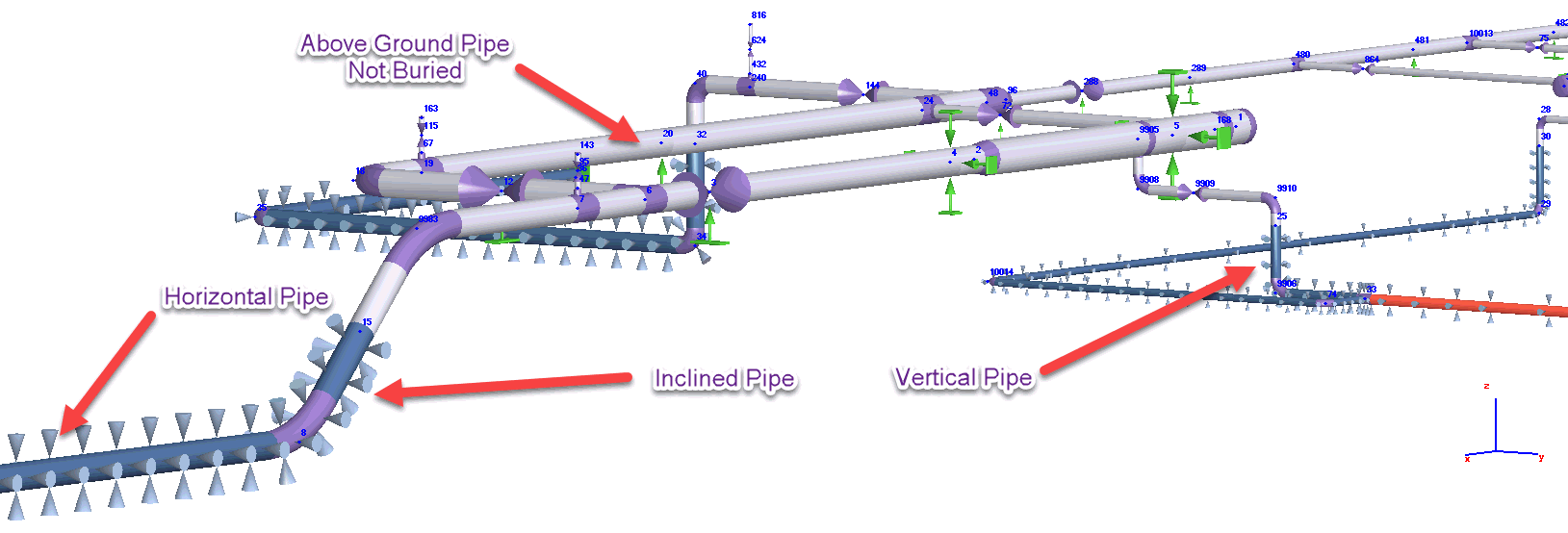
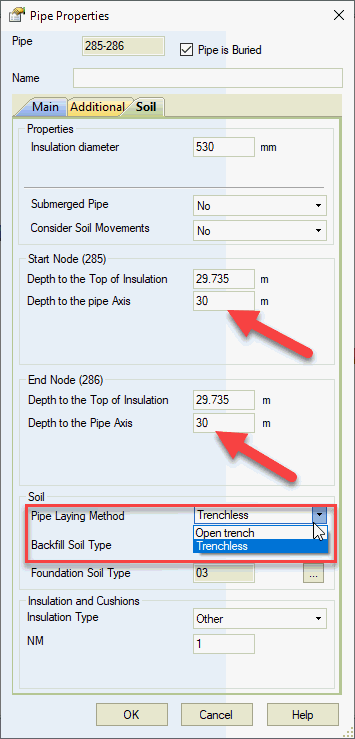
It can easily deal with the pipelines buried in the dry soil, submerged in the liquefied soil, considering the expansion cushions and insulation stiffness, ballasting weights, horizontal, vertical, inclined pipes, combined buried and above ground (not buried) piping model, seismic wave propagation analysis, landslide, soil subsidence, seismic fault crossing, consider the natural arch of collapse for horizontal directional drilling method.
2 Buried Pipeline Model for Dry Soil
2.1 Lateral Bearing Zone #1 (Unrestrained)
2.2 Axial Sliding Zone #2 (Unrestrained)
2.3 Restrained Zone #3
2.4 Restrained and Unrestrained Zones
3 Buried Submerged Pipeline Model for Liquefied Soil
3.1 General Soil Model for Submerged Pipelines
3.2 Water Buoyancy
3.3 Liquefied Soil Properties
4.1 General Soil Support Description
4.2 Soil Support Model for Horizontal, Vertical and Inclined Pipes
5 Modeling of Soil Subsidence, Frost Heaving, Landslide, Seismic Fault Crossing
6 Longitudinal Soil Spring Properties
6.1 Bilinear Spring Model
6.2 Friction Force for District Heating Networks Calculation (EN 13941-2019, CJJ/T 81-2013, GOST R 55596-2013)
6.3 Friction Force for Gas and Oil Pipelines Calculation (ASME B31.4, B31.8, B31.12, CSA Z662, BS PD 8010, SNIP, SP, GOST)
6.4 Natural Arch of Collapse Phenomena
7 Lateral Soil Spring Properties
8 Vertical Soil Spring Properties
9 Ring Bending Stress Calculation
9.1 Ring Bending Stress from the Soil Weight
8.2 Pipe Strength Against the Surface Load
9.3 Polyurethane (PUR) Insulation Stress Analysis
10 Seismic Wave Propagation Analysis
11 References
Interaction between the pipeline and surrounding soil is analyzed using methods developed by A.B. Aynbinder for START-PROF (at that time called "ST-01"). Methods are based on various experimental and theoretical research conducted at VNIIST (Moscow) and other organizations, and is a version of methods described in [1] and [6]. This soil model is widely used in all Russian and CIS companies for dry and submerged pipelines (in rivers, lakes etc.) since 1982 and integrated in 5 (five) piping stress analysis software packages used in that region.
START-PROF soil model consider:
Various non-linear empirical soil resistance to pipe displacement in vertical, horizontal and longitudinal directions
Affect of polyurethane foam insulation stiffness
Affect of horizontal cushioning pad thickness
Change in the properties of suspended soil in flooded sections
Vertical buoyancy force in flooded sections
Change in soil resistance force in horizontal, vertical and inclined pipe sections
Increased number of soil springs in the area of strong longitudinal and transverse displacements
START-PROF uses a beam pipeline model, where continuous interaction between pipeline and soil is modeled with the discrete bilinear springs, placed at certain intervals (fig. 1).
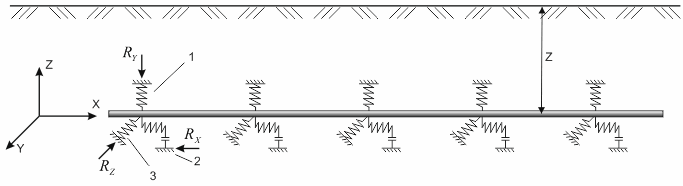
1 - Vertical soil spring, 2 - Axial soil spring, 3 - Lateral soil spring
Fig. 1. Pipeline and soil interaction model
START-PROF has two different soil support placing algorithms:
For buried pipeline in the dry soil

For submerged buried piping in liquefied soil with ballasting weights



The main goal of this model is to save on the number of supports in whole model to increase analysis speed without loss of calculation result accuracy.
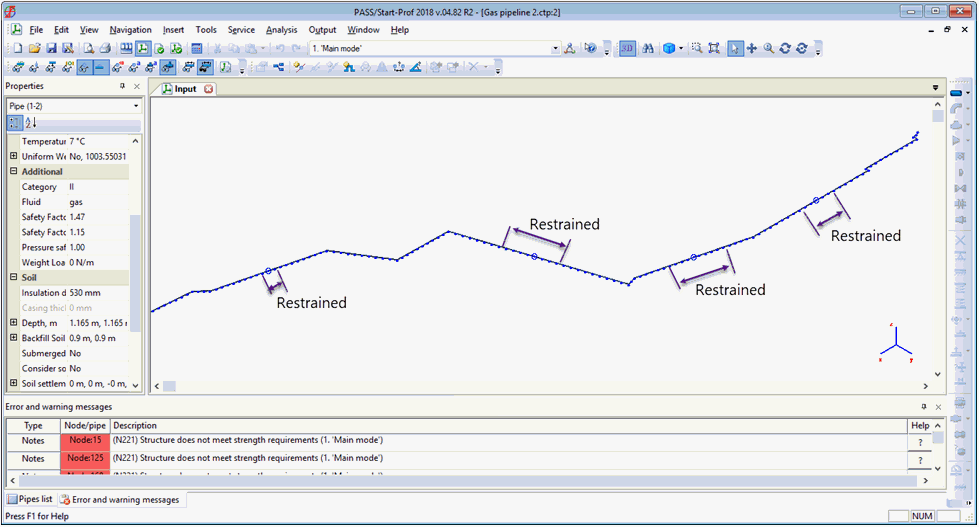
Springs are placed automatically. Three zones are marked around the nodes where supports are more closely placed (fig. 2):
Zone #1: lateral bearing zone (unrestrained) with the length of Lb. Four supports are placed at equal distance
Zone #2: axial sliding zone (unrestrained) with the length of La. Four supports are placed at a distance increasing exponentially from zone #1 to zone #3
Zone #3: Restrained zone. Supports are placed at 100D spacing, where D - pipe external diameter
The weight of pipeline, insulation and product is automatically removed to avoid the huge deflections in 100D pipe spans. This the sum of pipeline, insulation, and product weights is used to calculate the soil springs properties including the friction force.
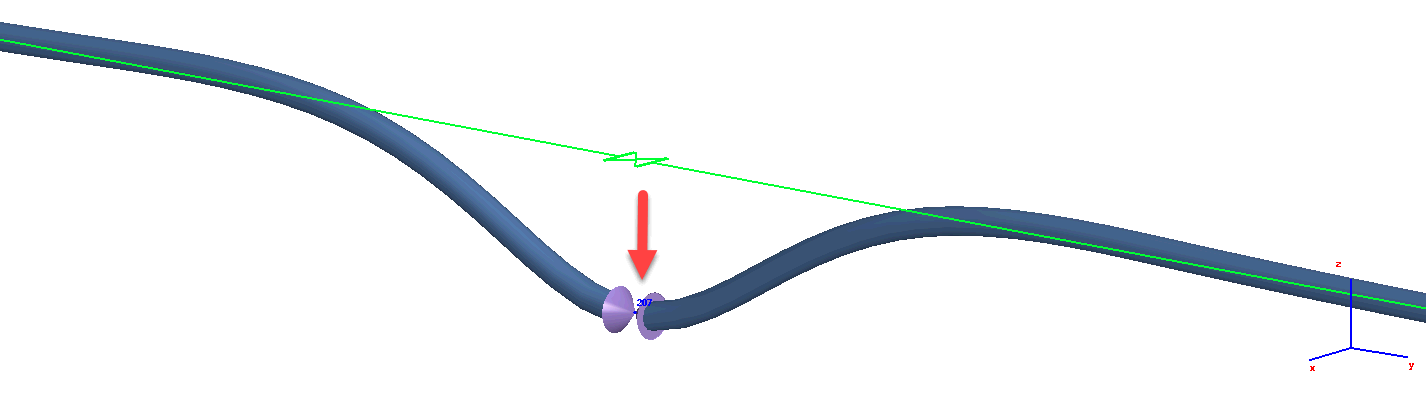
But if you will add the heavy valve on buried pipeline, the weight of the valve will be considered and you will see the deflections:
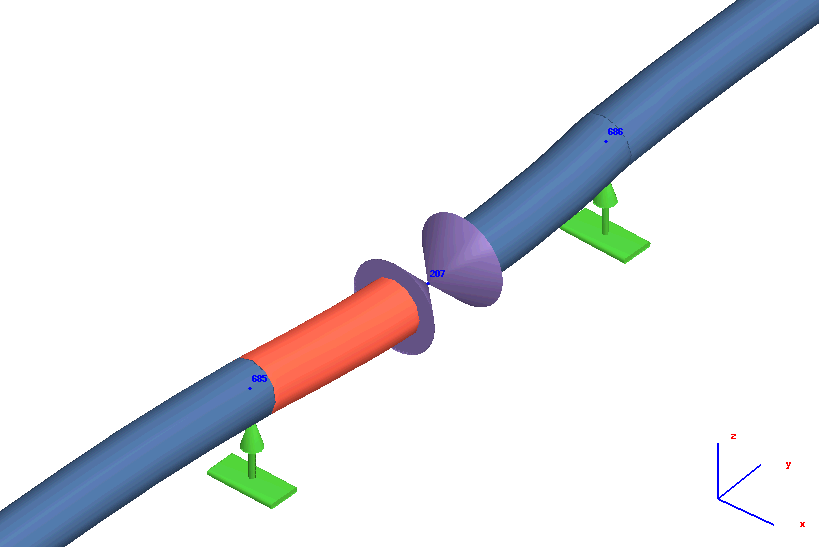
Also you can add the supports. It doesn't affect the accuracy of the soil model:
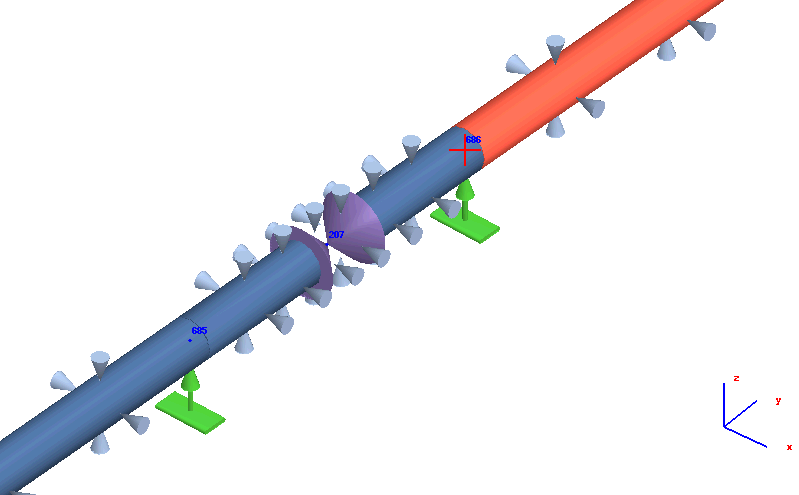
It is possible to manually increase the condensation of soil springs to increase the result accuracy:


If several operating modes are specified in operation mode editor, then first sustained operating mode is used for La and Lb calculation and these values are used for all operating modes.
The number of supports in the area of strong longitudinal and transverse displacements is increased automatically; i.e., nodes:
with a tee
with any bend
with a pipe axis change
with any expansion joint
with pre-stretch
with linear displacement
with a free end
with a resting support with an input displacement
with a guiding support with an input displacement
with an fixed anchor with an input displacement
with a restraint with an input displacement
with a valve
at the border with an above-ground element
at the border between elements with and without subsidence
in some other cases, when needed
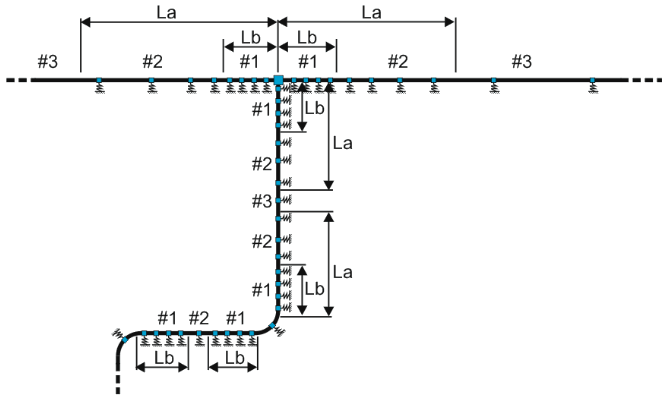
Fig. 2. Placement of supports modeling soil interaction
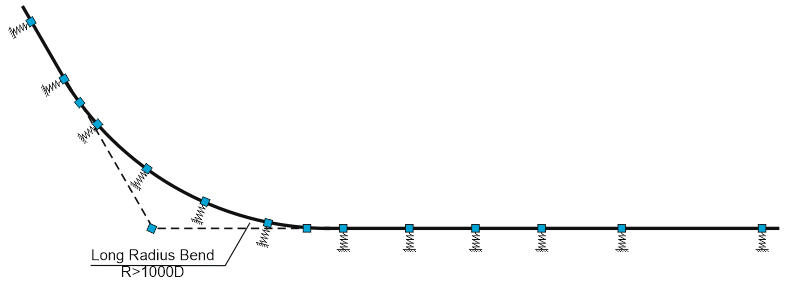
Placement of supports on long radius bends
Lateral bearing zone #1 have a big bending deformations and transverse displacement (fig. 3). To increase model accuracy, four soil springs are automatically placed here.
lateral bearing length is calculated automatically using the following:
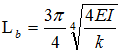 ,
,
where
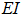 -
pipe bending stiffness,
-
pipe bending stiffness,
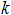 -
soil stiffness factor.
-
soil stiffness factor.
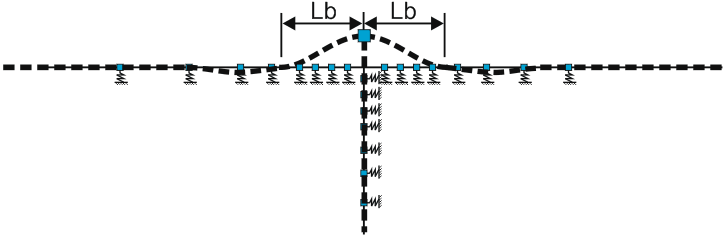
Fig. 3. Bend zone #1
Axial sliding zone #2 have a big longitudinal deformations and displacements (La on the fig. 4). To increase model accuracy, supports are placed with exponential increasing spacing from zone #1 to zone #3.
See also Restrained and Unrestrained Zones

Virtual anchor length for an elastic-plastic soil model [6] can be calculated using equation (see details here):
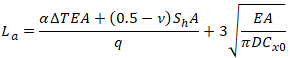
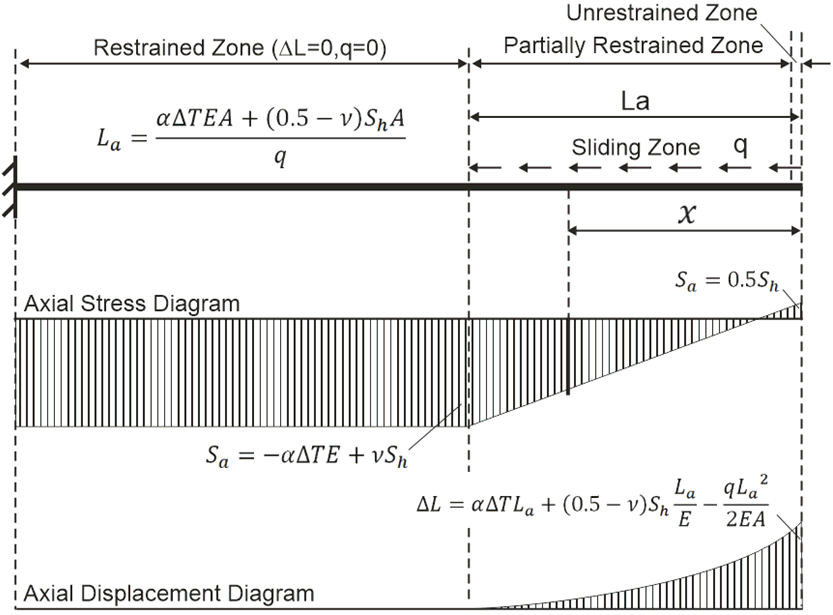
Fig. 4. Sliding zone #2
There is no bending and no axial displacements in the restrained zone. Therefore, soil springs are placed at a large spacing, equal to 100D
See also Restrained and Unrestrained Zones
ASME B31.4, ASME B31.8, ASME B31.12, CSA Z662, BS 8010 codes divides the pipeline into "Restrained" (#3) and "Unrestrained" (???) zones with different strength criteria unlike EN 13941, GOST, SNIP, SP codes that doesn't divide pipeline into such zones and has universal strength criteria suitable for both of them. The main problem for every pipeline designer: how to find the virtual anchor points and divide pipeline into restrained and unrestrained zones? The START-PROF software will save you from manually searching for these zones. Read here how START-PROF deal with it.
For submerged buried pipeline START-PROF adds the soil springs with the span equal to 5D. The weight of pipeline, insulation and product is not removed to get the accurate results with the ballasting. Ballasting weight can be added to the pipeline:
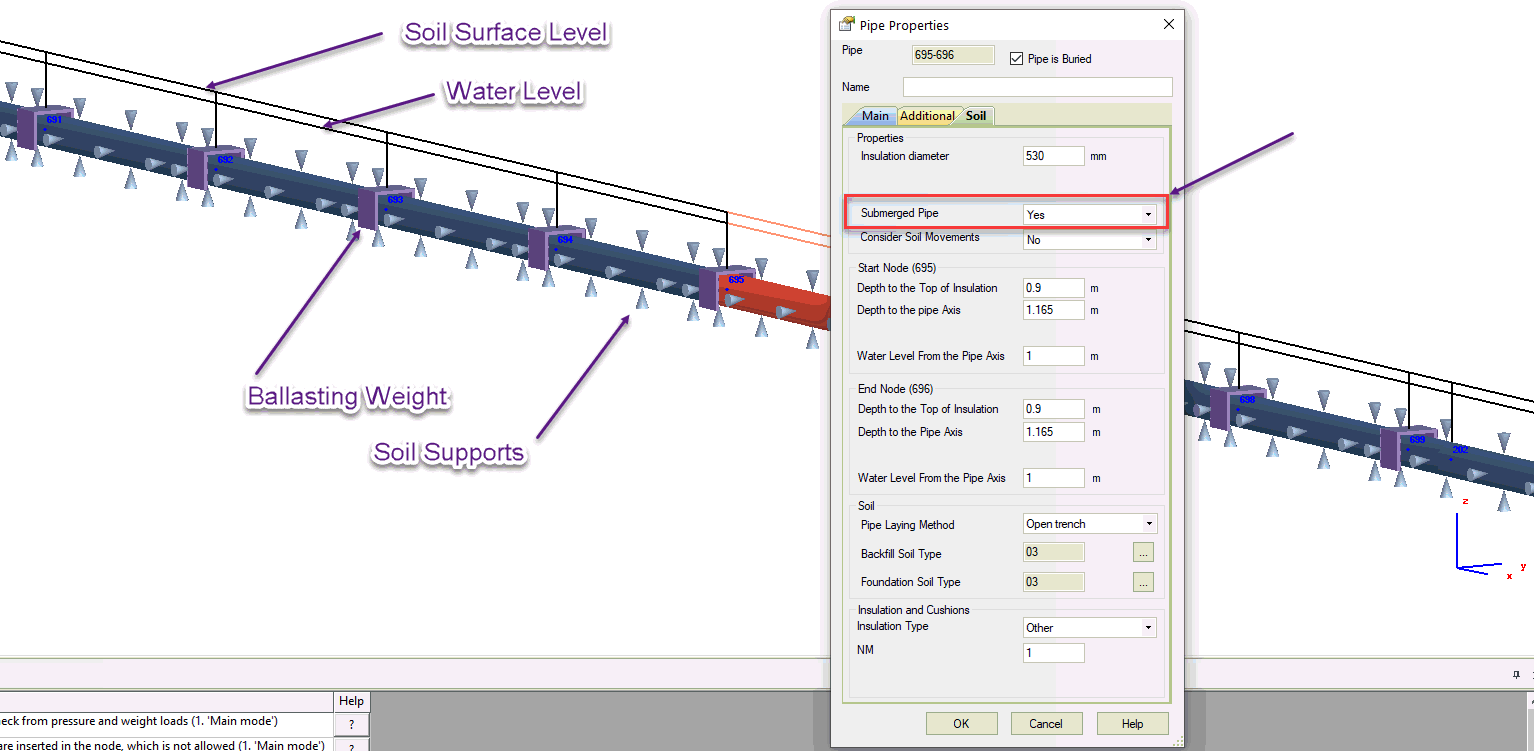
Buoyancy acting on the pipe is automatically considered depending on the water level. For horizontal, vertical and inclined pipe elements, buoyancy calculate only for the pipe section part which is under teh water level (fig. 8).
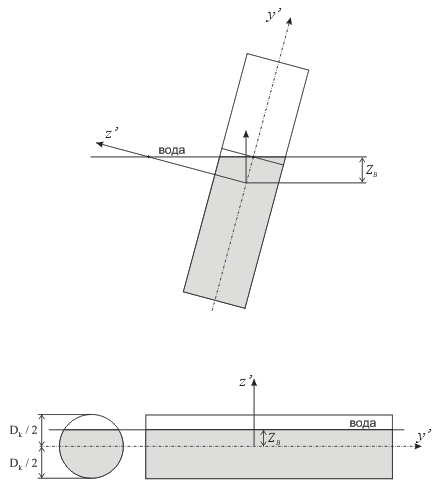
Fig. 8. Calculation of the volume of displaced liquid for buoyancy analysis
START-PROF automatically calculates the properties of the liquefied soil (suspended soil particles in the water). Please see soil spring property description below
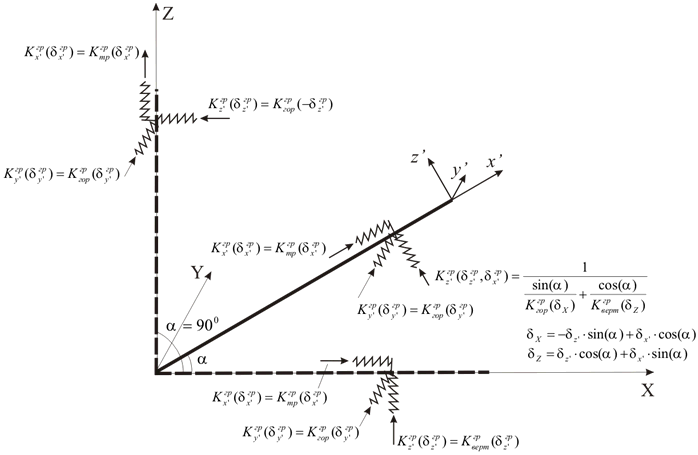
Each soil support consist of vertical, horizontal and longitudinal springs (fig. 5).
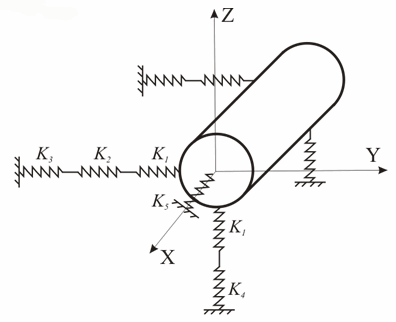
Fig. 5. Accounting for the stiffness of the PUR-insulation layer and expansion cushion pads
Stiffness K1 is a non-linear function dependent on expansion cushion deformation according to [3]. Presence or absence of expansion cushions is set in buried element properties.


Stiffness K2 is a non-linear function dependent on Polyurethane foam (PUR) layer deformation according to [3]. To calculate PUR stiffness, insulation casing diameter must be specified in the buried element properties.
Stiffness of soil springs depends on their direction (fig. 5). There are three types:
springs in lateral direction in the horizontal plane (horizontal soil resistance) K3
springs in vertical direction (vertical soil resistance) K4
springs longitudinal springs (longitudinal soil resistance) K5
The general model of algorithms for the correlation of reactions in springs and displacement is shown on fig. 4. The algorithm values are calculated based on input buried element properties, as well as base and back-fill soil properties set in the soil database.
Springs restricting lateral displacement in the horizontal plane K3 have a reaction and displacement correlation shown on fig. 6.a. Vertical and longitudinal springs are shown on fig. 6.b and fig. 6.c, respectively according to [1] and [6].
After starting an analysis, START-PROF automatically runs a series of consecutive analyses and at each step clarifies the stiffness value of all springs K1, K2, K3, K4 and K5. When a certain accuracy is achieved, the analysis is stopped.
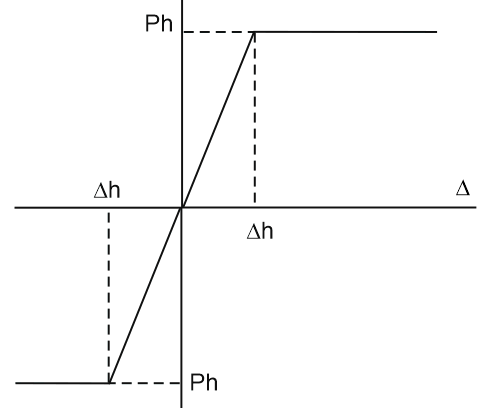
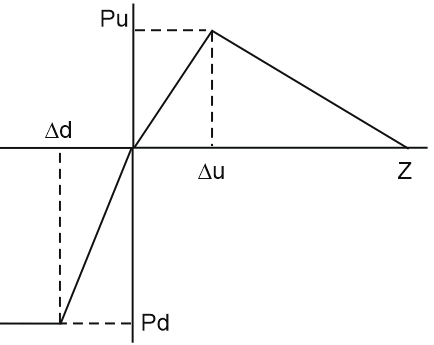
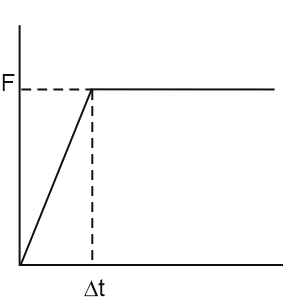
Fig. 6. Bilinear soil resistance vs displacement diagrams of K3, K4, K5
Depth, water height and subsidence can change along the pipe length
User should specify the properties at the one end of the pipe ZH, HBH, ΔH and on the other end of the pipe ZK, HBK, ΔK (fig. 6).
Note: Depth, water height and subsidence are stored in node object properties, not in pipe element. So these values must be the same for a node, even if it belongs to two adjoining elements. For example, if depth changes for a node of one element, depth will automatically change for this node of the other adjoining element.
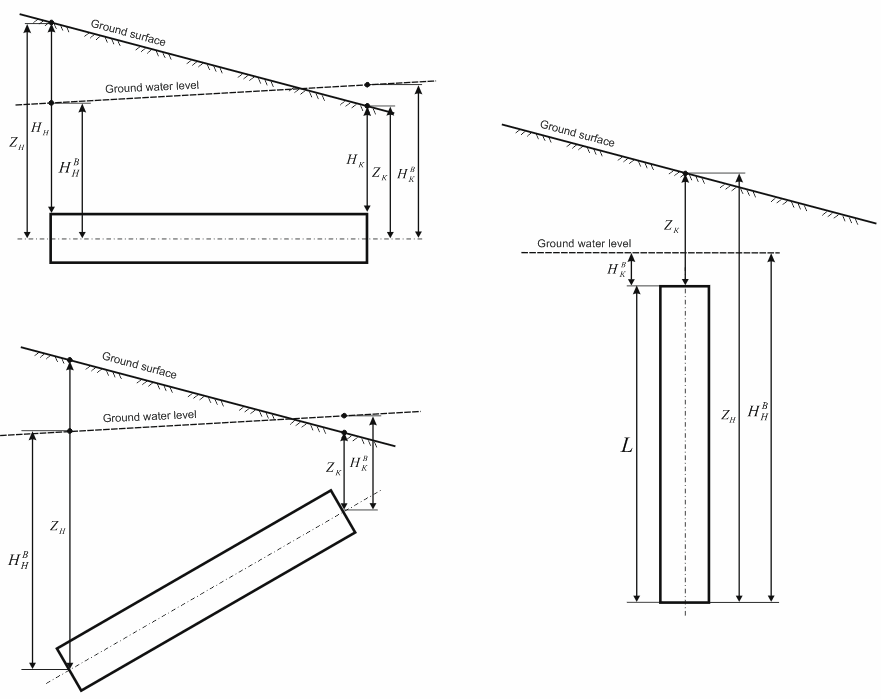
Fig. 6. Depth and water height based on element length
For inclined and vertical pipes the bilinear properties of each soil spring (stiffness, water buoyancy, spring displacement etc.) are calculated using individual depth of the specific spring (fig. 7). Various depth Zi and water height HBi values determined by linear iteration of start and node nodes ZH and ZK are used (fig. 7) when calculating the stiffness K3, K4 and K5. Water buoyancy is also calculated based on water height HBi at each point. Subsidence (spring displacement) value for each spring Δi is calculated in a similar way, using linear iteration ΔH, ΔK.

Fig. 7. Spring depth calculation
Stiffness of the springs K3, K4 and K5 are also depend on the pipe angle to the horizontal plane (from 0 to 90 degrees). For vertical pipe elements the vertical stiffness K4 behavior becomes the same as behavior of horizontal spring K3. Also, if the expansion cushions are present, the spring stiffness K1 is added to the vertical spring K4.
Due to this, START-PROF can easily calculate the piping model with
When the soil subsides, for example, due to thawing of base soil or mining, there is no resistance from the pipeline base and it subsides along with the soil (fig. 9).
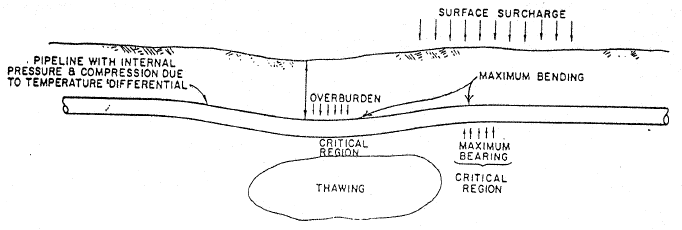
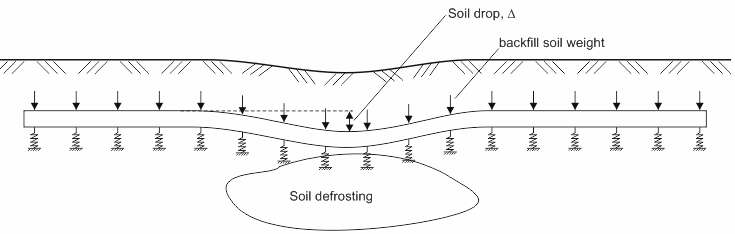
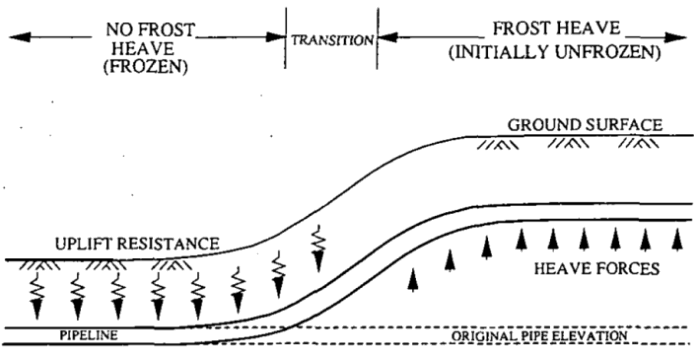
Fig. 9. Pipeline with soil subsidence and frost heaving
The subsidence process can be described using the correlation model shown on fig. 6.b and shifting it to the left by the value of base subsidence Δ (fig. 10). This model is equivalent to the displacement of the soil support downward on the distance Δ (fig. 9).
The value of subsidence due to melting or compression of base soil layers is determined using the methods from the code (for example SNIP [5]) or using the special software like BOREY, FROST 3D and other.
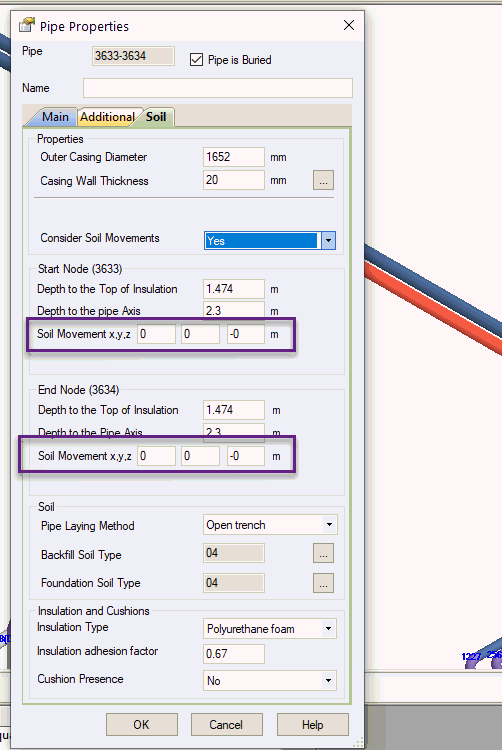
To model the soil subsidence we should specify the -Z direction soil movement in the pipe buried properties.
To model the opposite effect "frost heave" (upward displacement), the soil movement should be positive, in +Z direction.
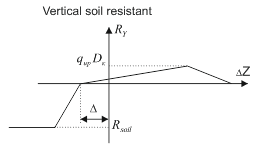
Fig. 10. Correlation of soil resistance to vertical displacement taking into account subsidence
To model the landslide, permanent ground deformation, vertical or horizontal seismic fault crossing etc. the soil displacement can be specified in all other directions (X, Y, Z) in the pipe buried properties.
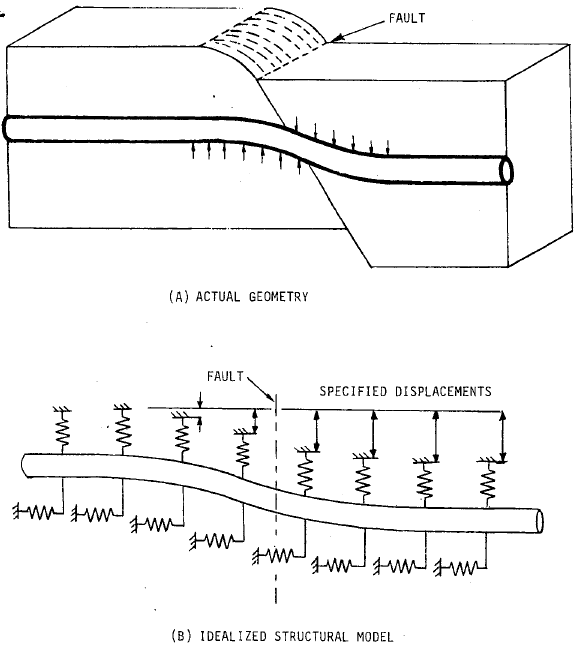
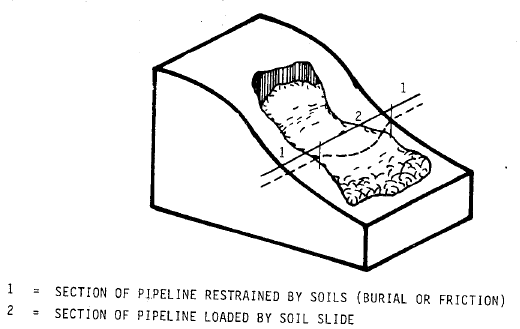
To check the strength of the pipeline during the landslide START-PROF offers the strain limit criteria according to the various codes ASCE 2001 ALA and other, that can be chosen in the operation mode editor.
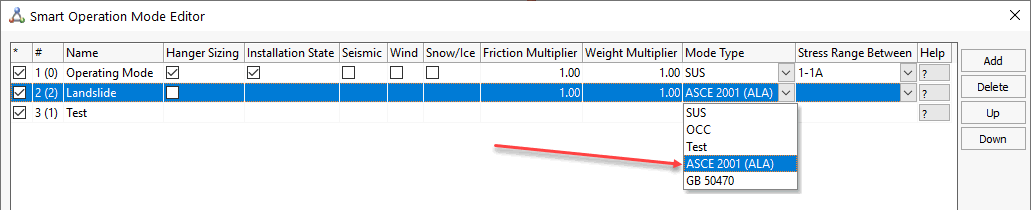
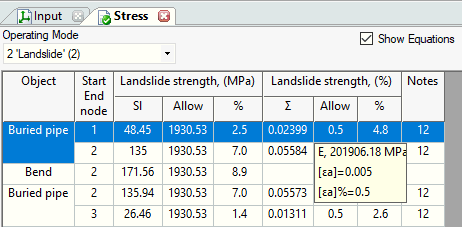

START-PROF soil database contain all needed values for soil spring property calculation:
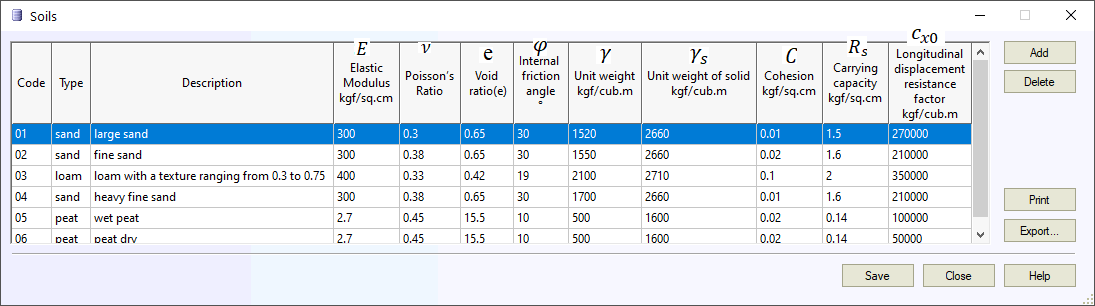
Soil resistance to vertical pipe displacement in the area of elastic-plastic deformation can be modeled as linear correlation, proposed by A.B. Aynbinder [1].
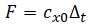
where
F - maximum allowable soil resistance to displacement, N/sm2, It is longitudinal friction force F, see the method of calculation below
cx0 - generalized tangent soil resistance factor N/sm3,
∆t - working displacement value corresponding to maximum soil resistance to displacement, cm.
This dependence is obtained by substituting the true diagram of soil resistance to longitudinal displacement (fig. 11.a) with an idealized bilinear diagram (fig. 11.b).
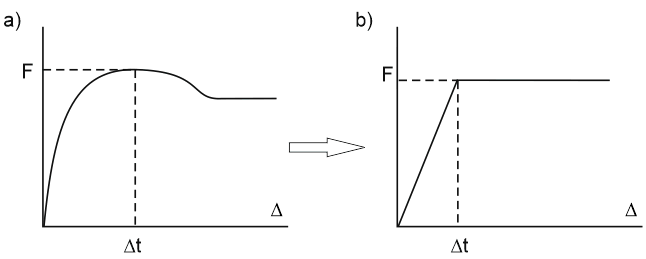
Fig. 11. Dependence of soil resistance to longitudinal displacement
Tangent soil resistance factor can be found as:
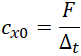
and has the dimensions of the soil bed factor. In the soil database this value is referred to as the resistance to longitudinal displacement factor. The factor shows the slant of the first section of the bilinear diagram, shown on fig. 11.b.
To input a rigid-plastic soil model without taking into account elastic resistance, the tangent resistance factor cx0 must have a very high value (fig. 12). In practice, a large number, for example 100000 tf/m3 can be used. If the database has the value cx0=0, then START-PROF uses a value equal to 100000 tf/m3.
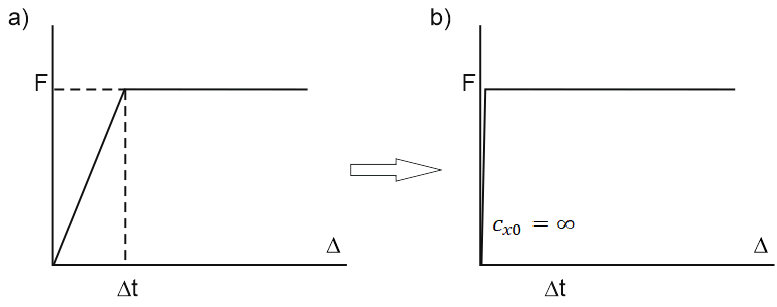
Fig. 12. Elastic-plastic and rigid-plastic soil models
Values of cx0 adapted from experimental data for various soil types are provided in table below
Generalized tangent soil resistance factor cx0 values, kgf/m3
Soil Type |
Liquidity Index IL |
Porosity Factor ε |
||||
|---|---|---|---|---|---|---|
<0.5 |
0.5-0.6 |
0.6-0.7 |
0.7-0.8 |
>0.8 |
||
| Coarse and medium gravel sand | - | 330000 | 300000 | 270000 | 250000 | - |
| Fine and silty sand | - | 250000 | 210000 | 210000 | 190000 | - |
| Sandy loam | 0 < IL ≤ 0.25 | 350000 | 330000 | 300000 | 300000 | 300000 |
| 0.25 < IL ≤ 0.75 | 350000 | 320000 | 300000 | 250000 | 250000 | |
| Loam | 0 < IL ≤ 0.3 | 380000 | 350000 | 350000 | 320000 | 300000 |
| 0.3 < IL ≤ 0.75 | 350000 | 330000 | 300000 | 250000 | 200000 | |
| Clay | 0 < IL ≤ 0.3 | 400000 | 380000 | 350000 | 330000 | 300000 |
| 0.3 < IL ≤ 0.75 | 450000 | 400000 | 350000 | 300000 | ||

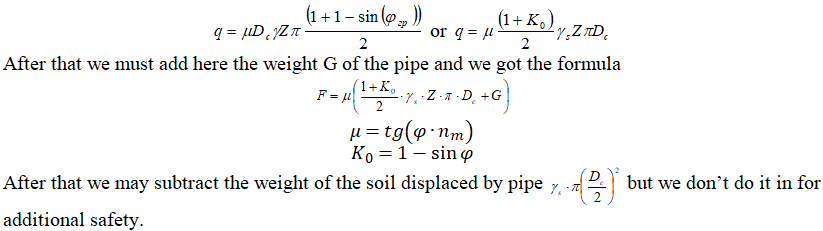

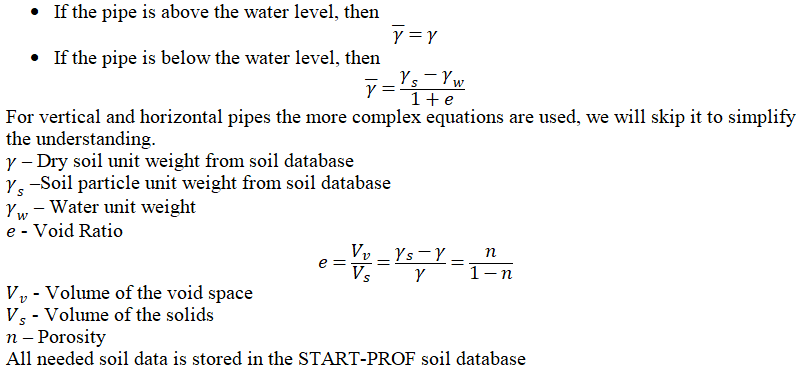
If open trench type laying is used, then chosen, then soil natural arch of collapse is not considered. The soil pressure on the pipe is calculated using whole depth. The friction force is calculated using classic equation:
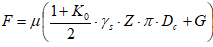
The soil pressure increases linearly with increasing depth.
If trenchless laying method is used, for example horizontal directional drilling, and the pipe depth is very high, then a self-supporting arch collapse forms above the pipe (natural arch of collapse).
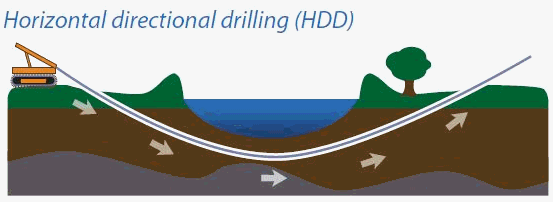
This arch supports all the soil pressure above itself.
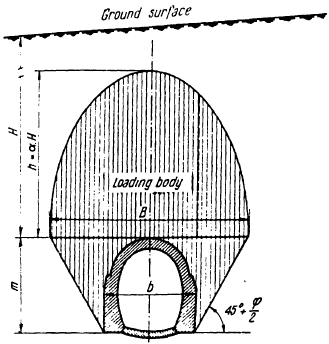
Only soil inside the natural arch of collapse produce the pressure on the pipe. The friction force, polyurethane foam insulation stress analysis, ring bending stress Calculation in the pipe in START-PROF are automatically calculated using consideration of natural arch of collapse. The reduced depth, depending on calculated dimensions of the natural arch of collapse, is used for calculation.
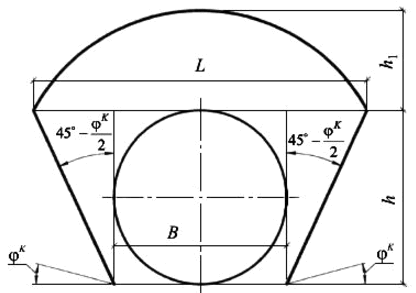

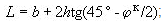




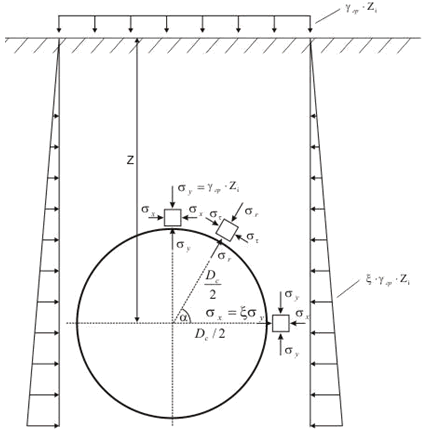
7.1 Rin g Bending Stress from the Soil Weight
See details here
Surface load can be represented by the two concentrated forces and uniform load along the line. See details here
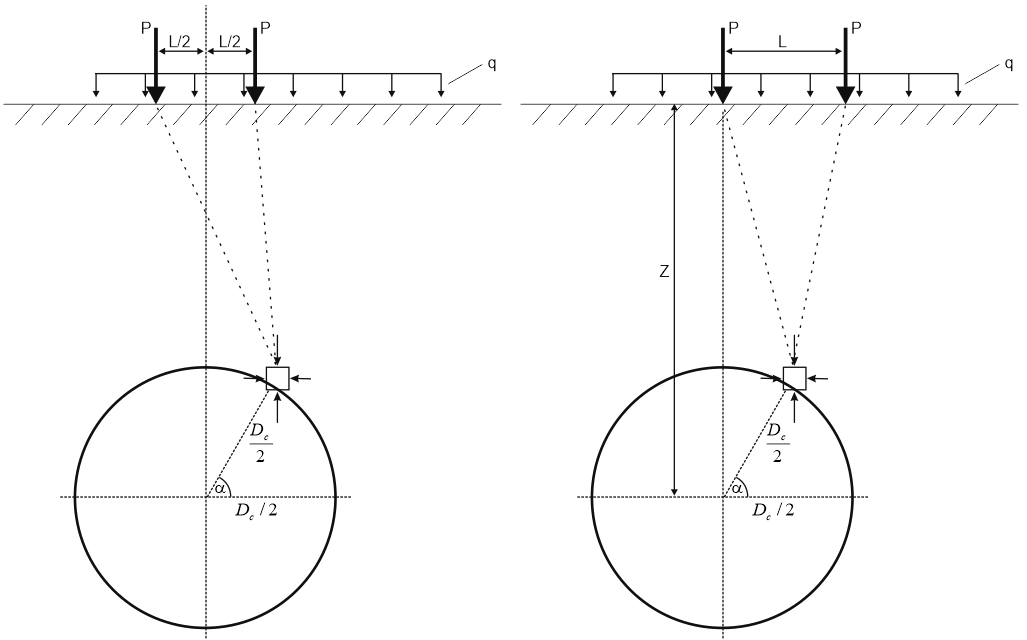
See details here


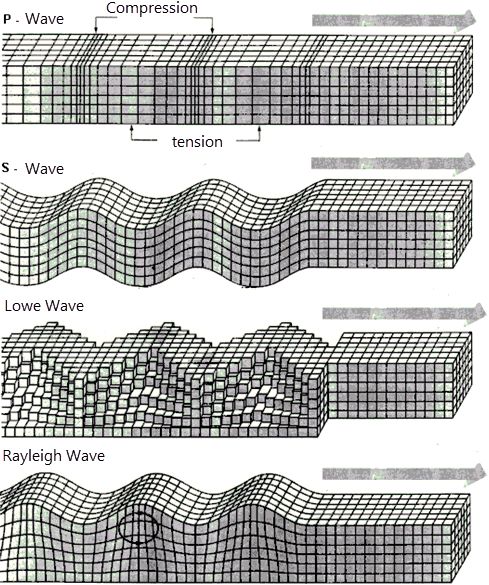
Analysis of the seismic wave propagation effect on the buried pipeline using START-PROF is described here
1. Aynbinder A., Kamerstein A. Analysis of the transmission pipelines for strength and stability. Moscow "Nedra" .1982
2. Skomorovsky Ya.Z., Ainbinder AB, longitudinal movement of buried pipelines taking into account physical nonlinearity soil shear resistance. Pipeline strength questions, Moscow 1975
3. Arbeitsblatt FW 401: Verlegung und static von KMR für Fernwärmenetze Arbeitsgemeinschaft Fernwärme- AGFW-e, V.- bei der Vereinigung Deutscher Elektrizitätswerke, 1992
4. Borodavkin P. Buried transmission pipelines (design and building), Мoscow "Nedra, 1982
5. SNiP 2.02.04–88. Foundations located on permafrost. Gosstroy USSR. Мoscow, 1991
6. Aynbinder A., Kamerstein A. Analysis of the transmission pipelines and flowlines for strength and stability. Мoscow "Nedra", 1991